A map reduce algorithm for connected components: implementation
At long last, a complete implementation of the algorithm I described some time ago.
You are kindly advised to go back and check the algorithm motivation and description in my older post, but the short of it is that it is a map reduce algorithm for connected components that is not sensitive to the diameter of the graph, a first at that time to the best of my knowledge. It works by merging subset of nodes that are connected by an edge and it does so in a highly parallel way — the number of subsets drops exponentially at each iteration, by \(1/2\) in expectation in the undirected version of the algorithm, in an adaptation of a pre-existing algorithm for the PRAM model.
As I discussed in a recent post, I got interested in Rhipe, an R library for Hadoop, and this is what we are going to use here. Wait, you are saying, a graph algorithm in a statistics oriented language? That's exactly right. First, I thought it would be more interesting to test R and Rhipe outside their confort zone of computational statistics. Second, in the same post I didn't find another Hadoop library that fit all my criteria, so Rhipe had to do. Third, the R community does not limit itself to statistics and machine learning, even if those are its fundamental strengths. In fact there are a graph package — graph — and even a graph drawing package — Rgraphviz. A couple more notes on the implementation. This is not production-ready code. For instance, I did not bother removing the various temp files, since I wanted to inspect them after the fact. There is also a counter update that is placed in the middle of a loop without much consideration for scalability. These are not fundamental problems and can be easily fixed. Moreover, you will see that I call multiple times the map reduce relational join about which I reported in this post. In fact, there are only two "custom" map reduce jobs involved here, one of which is trivial and I think this supports the idea that the relational join is an important abstraction for map reduce programs, not just a case of SQL-envy. And without further ado, the program:
Line 1
The signature has three arguments, the graph itself, the forest used to represent node sets that will evolve into connected components and recursion level that is used to control pseudo-random choices in a coordinate fashion across processes. The second and third argument need not be provided by the end user, they are only useful for recursive calls. Graphs are represented as lists of lists with two elements, named "from" and "to" — albeit this algorithm is for undirected graphs.
Lines 2–6
Some temp files. I do not remove them in this implementation, but in production you should.
Lines 8–20
On the first call, the forest is not provided. Initialize it with the trivial forest, one node per tree — here self-loops mark the root in a slight departure from standard forests.
Lines 22–34
With two simple joins, create a combined view of the graph and the forest where each record contains one edge of the graph and the parents in the forest for each of the end-nodes.
Line 36
The only "custom" map reduce job of interest in the whole program, update_parent makes the actual decisions on what node subsets are going to be merged. It returns the number of live edges, edges that bridge two subsets. When this is 0 — actually, NULL in the implementation — we are done. I will explain this after the main program.
Line 37
This check tells us we are done.
Line 38
Trace the decline in the number of live edges, just for my education.
Line 40–46
Merge some pairs of trees in the forest as already decided at line 36. This actually executes the merger and can be easily expressed as a join.
Lines 48–54
This modifies the forest to go from a max depth of 2 back to 1 as we started with. You guessed, it's just another join, this time of the self- variety.
Lines 55–56
Recurse or return the forest. It's tail recursion, the algorithm is iterative, but we don't do loops unless we have to. It's a matter of style.
The next function is the implementation of the update_parent function above.
Line 1
This function takes in input the combined graph-forest view and outputs a list of edge updates for the forest into its ofolder argument. It also needs a round number that is used to generate correlated pseudorandomness across tasks.
Lines 2–5
The function consists of one map reduce job with said input and output files.
Lines 6–24
The mapper randomly assigns a pseudo-random binary label to each node that depends only on the node itself and the round number. Then it checks that the two nodes defining an edge belong to different trees in the forest (liveness) and that they have different pseudo-random labels. If so it emits a key, value pair that represents an edge from the root of one tree to the other, keyed on the origin node, which is like a green light to merging the two trees.
Lines 25–28
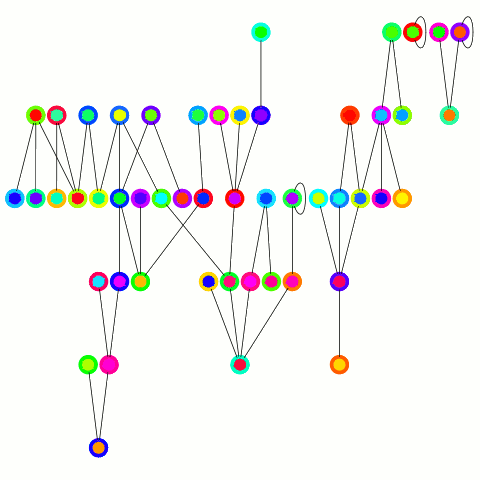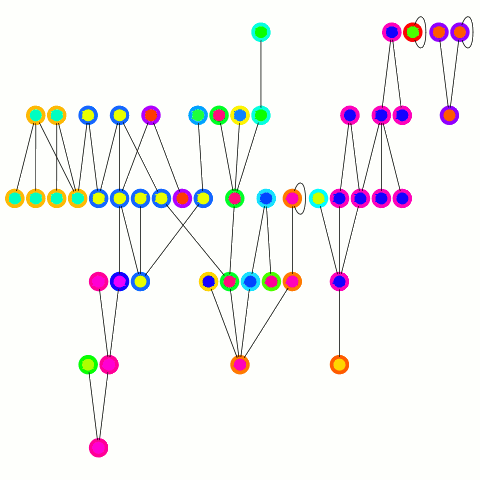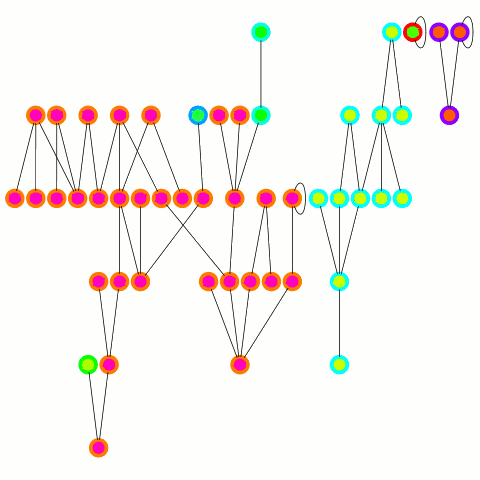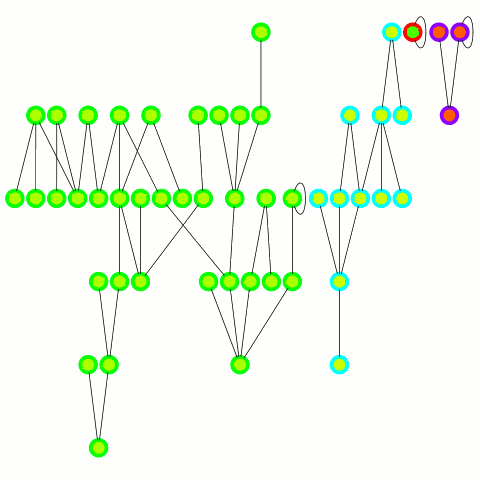
The reducer just arbitrarily picks one of these update edges per tree. One tree can only merge into another one during one round; on the other hand the "receiving" tree can accept many trees — it's an asymmetrical merge. This is equivalent to the arbitrary CRCW PRAM model in the original PRAM algorithm from which this is derived and allows to use a combiner, which is important in case of high degree nodes. An animation depicting the algorithm's working is below.
One detail: if you are going to try this at home, my setup is Ubuntu maverick, R 2.11.1, Rhipe 0.65.4 and CDH3. With this setup, to avoid what I suppose is a Rhipe bug, one needs to specify certain map reduce options to rhmr, specifically
Epilogue
In all of 85 lines — and I didn't skimp on line breaks to get there — we have implemented a non-trivial, scalable algorithm in the map reduce framework. You could factor in the 77 lines that went into implementing joins, but that would grossly underestimate the reusability of that abstraction, which is provided by several languages and libraries for map reduce independent of this algorithm, or even graph algorithms in general. Readability is in the eye of the beholder, but if you are used to moving around functions as first class objects and are basically familiar with map reduce, I hope this code is reasonably clear.
Besides an implementation for the algorithm presented in an older post, the present post also provides a beefier Rhipe exercise as I had promised in a review post of map reduce libraries and languages. Therein I had also anticipated the following friendly challenge, where to take part is to win: can anyone implement this algorithm in any of the alternative map reduce environments? The list includes, but doesn't have to be limited to: Java/Hadoop, Java/Cascading, C++/Pipes, Python/Dumbo, Pig, Hive and Cascalog. Is it possible? How hard is it? Can we learn anything comparing two implementations? This is not wordcount and I suspect we stand to learn a lot more from the comparison of implementations of a non-trivial algorithm.
You are kindly advised to go back and check the algorithm motivation and description in my older post, but the short of it is that it is a map reduce algorithm for connected components that is not sensitive to the diameter of the graph, a first at that time to the best of my knowledge. It works by merging subset of nodes that are connected by an edge and it does so in a highly parallel way — the number of subsets drops exponentially at each iteration, by \(1/2\) in expectation in the undirected version of the algorithm, in an adaptation of a pre-existing algorithm for the PRAM model.
As I discussed in a recent post, I got interested in Rhipe, an R library for Hadoop, and this is what we are going to use here. Wait, you are saying, a graph algorithm in a statistics oriented language? That's exactly right. First, I thought it would be more interesting to test R and Rhipe outside their confort zone of computational statistics. Second, in the same post I didn't find another Hadoop library that fit all my criteria, so Rhipe had to do. Third, the R community does not limit itself to statistics and machine learning, even if those are its fundamental strengths. In fact there are a graph package — graph — and even a graph drawing package — Rgraphviz. A couple more notes on the implementation. This is not production-ready code. For instance, I did not bother removing the various temp files, since I wanted to inspect them after the fact. There is also a counter update that is placed in the middle of a loop without much consideration for scalability. These are not fundamental problems and can be easily fixed. Moreover, you will see that I call multiple times the map reduce relational join about which I reported in this post. In fact, there are only two "custom" map reduce jobs involved here, one of which is trivial and I think this supports the idea that the relational join is an important abstraction for map reduce programs, not just a case of SQL-envy. And without further ado, the program:
function(E, F_ = NULL, i =0) {
T1 = tempfile()
T2 = tempfile()
Fupdate = tempfile()
Fnew = tempfile()
Ftemp = tempfile()
if (is.null(F_)) {
#create trivial forest
F_ = tempfile()
rhex(
rhmr(
ifolder = E,
ofolder = F_,
map = expression({lapply(map.values, function(v) {
rhcollect(as.integer(v$from), NULL)
rhcollect(as.integer(v$to), NULL)})}),
reduce = expression(post = {rhcollect(reduce.key, list(from = reduce.key, to = reduce.key))}),
inout = c("sequence", "sequence")))}
#merge graphs and forest
rhreljoin (ileftfolder= E,
irightfolder= F_,
ofolder=T1,
map.left.key = function(k,v) as.integer(v$from),
map.right.key = function(k,v) as.integer(v$from),
reduce.value = function(k,ve,vf) list(parentfrom = vf$to, from = ve$from, to = ve$to))
rhreljoin (ileftfolder= T1,
irightfolder= F_,
ofolder=T2,
map.left.key = function(k,v) as.integer(v$to),
map.right.key = function(k,v) as.integer(v$from),
reduce.value = function(k,vt1,vf) list(parentfrom = vt1$parentfrom, parentto = vf$to, from = vt1$from, to = vt1$to))
#find component merge candidates
live_edges = update_parent (ifolder= T2, ofolder= Fupdate, i)$counters$live_edges
if (!is.null(live_edges)) {
print(paste("live edges:", live_edges))
#forest update
rhreljoin (ileftfolder= F_ ,
irightfolder= Fupdate,
leftouter= T,
map.left.key = function(k,v) as.integer(v$from),
map.right.key = function(k,v) as.integer(v$from),
reduce.value= function(k,vl,vr) if(is.na(vr)) {vl} else {vr},
ofolder= Ftemp)
#depth-reducing step
rhreljoin (ifolder= Ftemp ,
ofolder = Fnew,
leftouter = T,
map.left.key = function(k,v) as.integer(v$to),
map.right.key = function(k,v) as.integer(v$from),
reduce.value= function(k,vl,vr) list(from = vl$from, to = if(is.na(vr$to)){vl$to} else {vr$to}))
#recursion
randmate(E, Fnew, i+1)}
else return (F_)
}
Line 1
The signature has three arguments, the graph itself, the forest used to represent node sets that will evolve into connected components and recursion level that is used to control pseudo-random choices in a coordinate fashion across processes. The second and third argument need not be provided by the end user, they are only useful for recursive calls. Graphs are represented as lists of lists with two elements, named "from" and "to" — albeit this algorithm is for undirected graphs.
Lines 2–6
Some temp files. I do not remove them in this implementation, but in production you should.
Lines 8–20
On the first call, the forest is not provided. Initialize it with the trivial forest, one node per tree — here self-loops mark the root in a slight departure from standard forests.
Lines 22–34
With two simple joins, create a combined view of the graph and the forest where each record contains one edge of the graph and the parents in the forest for each of the end-nodes.
Line 36
The only "custom" map reduce job of interest in the whole program, update_parent makes the actual decisions on what node subsets are going to be merged. It returns the number of live edges, edges that bridge two subsets. When this is 0 — actually, NULL in the implementation — we are done. I will explain this after the main program.
Line 37
This check tells us we are done.
Line 38
Trace the decline in the number of live edges, just for my education.
Line 40–46
Merge some pairs of trees in the forest as already decided at line 36. This actually executes the merger and can be easily expressed as a join.
Lines 48–54
This modifies the forest to go from a max depth of 2 back to 1 as we started with. You guessed, it's just another join, this time of the self- variety.
Lines 55–56
Recurse or return the forest. It's tail recursion, the algorithm is iterative, but we don't do loops unless we have to. It's a matter of style.
The next function is the implementation of the update_parent function above.
function(ifolder, ofolder, mrround)
rhex(
rhmr(
ifolder= ifolder,
ofolder = ofolder,
map = eval(
substitute(
expression({
library(digest)
is.high = function(x,r) {
as.integer(
paste("0x", substr(digest(c(x,r)), 1,1), sep = ""))%%2 == 1}
lapply(map.values,
function(v){
if(v$parentfrom != v$parentto) {
rhcounter("live_edges", "live_edges", 1)
hfrom = is.high(v$parentfrom, mrround);
hto = is.high(v$parentto, mrround);
if (hfrom != hto) {
if (hfrom) {
rhcollect(v$parentfrom,list(from = v$parentfrom, to = v$parentto))}
else {
rhcollect(v$parentto, list(from = v$parentto, to = v$parentfrom))}}}})}),
list(mrround = mrround))),
reduce = expression(
post = {rhcollect(reduce.key, reduce.values[[1]])}),
inout = c("sequence","sequence"),
combiner = T))
Line 1
This function takes in input the combined graph-forest view and outputs a list of edge updates for the forest into its ofolder argument. It also needs a round number that is used to generate correlated pseudorandomness across tasks.
Lines 2–5
The function consists of one map reduce job with said input and output files.
Lines 6–24
The mapper randomly assigns a pseudo-random binary label to each node that depends only on the node itself and the round number. Then it checks that the two nodes defining an edge belong to different trees in the forest (liveness) and that they have different pseudo-random labels. If so it emits a key, value pair that represents an edge from the root of one tree to the other, keyed on the origin node, which is like a green light to merging the two trees.
Lines 25–28
The reducer just arbitrarily picks one of these update edges per tree. One tree can only merge into another one during one round; on the other hand the "receiving" tree can accept many trees — it's an asymmetrical merge. This is equivalent to the arbitrary CRCW PRAM model in the original PRAM algorithm from which this is derived and allows to use a combiner, which is important in case of high degree nodes. An animation depicting the algorithm's working is below.
One detail: if you are going to try this at home, my setup is Ubuntu maverick, R 2.11.1, Rhipe 0.65.4 and CDH3. With this setup, to avoid what I suppose is a Rhipe bug, one needs to specify certain map reduce options to rhmr, specifically
mapred = list(mapreduce.fileoutputcommitter.marksuccessfuljobs = "false").Annoying to figure out but not hard to work around. Most of this post was prepared with older versions of everything with which this problem did not manifest itself, and hopefully it will be fixed soon.
Epilogue
In all of 85 lines — and I didn't skimp on line breaks to get there — we have implemented a non-trivial, scalable algorithm in the map reduce framework. You could factor in the 77 lines that went into implementing joins, but that would grossly underestimate the reusability of that abstraction, which is provided by several languages and libraries for map reduce independent of this algorithm, or even graph algorithms in general. Readability is in the eye of the beholder, but if you are used to moving around functions as first class objects and are basically familiar with map reduce, I hope this code is reasonably clear.
Besides an implementation for the algorithm presented in an older post, the present post also provides a beefier Rhipe exercise as I had promised in a review post of map reduce libraries and languages. Therein I had also anticipated the following friendly challenge, where to take part is to win: can anyone implement this algorithm in any of the alternative map reduce environments? The list includes, but doesn't have to be limited to: Java/Hadoop, Java/Cascading, C++/Pipes, Python/Dumbo, Pig, Hive and Cascalog. Is it possible? How hard is it? Can we learn anything comparing two implementations? This is not wordcount and I suspect we stand to learn a lot more from the comparison of implementations of a non-trivial algorithm.
Ken, glad you enjoyed it, if this distance matrix permutation problem has any general relevance I would love to get a pointer to a description.
Start with the edge-list (all a->b pairs) of the graph. As you encounter each edge, if the two are in different trees, merge the trees. Here's a simplistic data structure that will do this, but if you want to be clever you can use a UnionFind http://en.wikipedia.org/wiki/Disjoint-set_data_structure data structure:
A - b,c,d
b A
c A
d A
E - f,g
F E
G E
Now if you notice, what you have at all times in that data structure is a forest of depth-one trees:
A E
b c d f g
Once the map phase concludes, just stream that out as an edge-list tree:
a b
a c
a d
e f
e g
and send to one reducer. The reducer runs *exactly the same algorithm* using the edgelist for each mapper's forest.
This requires
* Only one reduce
* O(N) memory in all phases
* Streams O(E) data through the mapper (which is cheap) but only O(N) data to the reduce